《剑指 Offer》算法题（20/68）

本文最后更新于：1 年前

旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组 {3, 4, 5, 1, 2} 为 {1, 2, 3, 4, 5} 的一个旋转，该数组的最小值为 1。

思路：
输入数组可以看成是两个递增数组的连接，其中第 2 个数组中的每一个值都不大于第 1 个数组中的任意一个值，且最小值是第 2 个数组的第 1 个值。
对于递增数组查询最小值，可以使用二分法查找。二分法涉及 3 个值，分别记为 a、b、c，分情况讨论——
（0）a > b > c，不存在；
（1）a < b < c，此时 a、b、c 都在后面数组，最小值是 a；
（2）a < b = c，此时 a、b、c 都在后面数组，最小值是 a；
（3）a = b < c，此时 a、b、c 都在后面数组，最小值是 a；
（4）a < b，b > c，此时 a、b 在前面数组，c 在后面数组，最小值在 b、c 之间，如果 b 是 c 的前一个元素，则最小值是 c；
（5）a = b，b > c，此时 a、b 在前面数组，c 在后面数组，最小值在 b、c 之间，如果 b 是 c 的前一个元素，则最小值是 c；
（6）a > b，b < c，此时 a 在前面数组，b、c 在后面数组，最小值在 a、b 之间，如果 a 是 b 的前一个元素，则最小值是 b；
（7）a > b，b = c，此时 a 在前面数组，b、c 在后面数组，最小值在 a、b 之间，如果 a 是 b 的前一个元素，则最小值是 b；
（8）a = b = c，如果 a、b、c 是连续的 3 个数，则最小值是 a；否则无法确定最小值所在区间，只能既查找 a、b 区间，也查找 b、c 区间，一旦在其中某个区间发现更小的值，就能够缩小查找范围。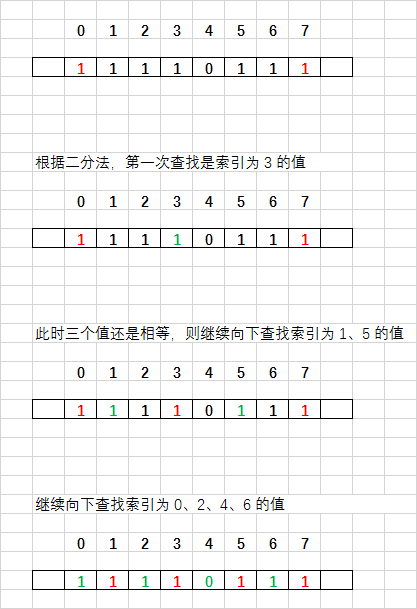

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
public int find(int[] arr) {
    int start = 0;
    int end = arr.length - 1;

    while (end > start) {
        int middle = ((end - start) >> 1) + start;

        // 合并（1）（2）（3）
        if ((arr[start] < arr[middle] && arr[middle] <= arr[end])
                || (arr[start] == arr[middle] && arr[middle] < arr[end])) {
            return arr[start];
        }

        // 合并（4）（5）
        if (arr[start] <= arr[middle] && arr[middle] > arr[end]) {
            if (end - middle == 1) {
                return arr[end];
            }
            start = middle + 1;
            continue;
        }

        // 合并（6）（7）
        if ((arr[start] > arr[middle] && arr[middle] <= arr[end])) {
            if (middle - start == 1) {
                return arr[middle];
            }
            end = middle;
            continue;
        }

        // （8）
        if (arr[middle] == arr[end] || arr[middle] == arr[start]) {
            if (middle - start == 1 && end - middle == 1) {
                return arr[start];
            }
            int[] range = findRange(arr, start, end);
            if (range[0] == range[1]) {
                return arr[range[0]];
            }
            start = range[0];
            end = range[1];
        }
    }

    return -1;
}

private int[] findRange(int[] arr, int start, int end) {
    int[] popArr = {start, end};

    while (true) {
        int[] pushArr = new int[(popArr.length << 1) - 1];
        pushArr[0] = popArr[0];
        for (int i = 0, j = 0, size = popArr.length; i < size - 1; i++) {
            Result result = getResult(arr, popArr[i], popArr[i + 1]);
            if (result.isFound()) {
                return result.getRange();
            } else {
                // 已经逐个查找了，还是没找到，说明数组从 start 到 end 的值都一样
                if (popArr.length > end - start) {
                    return new int[]{start, start};
                }
                int middle = result.getMiddle();
                pushArr[++j] = middle;
                pushArr[++j] = popArr[i + 1];
            }
        }
        popArr = pushArr;
    }
}

private Result getResult(int[] arr, int start, int end) {
    int middle = ((end - start) >> 1) + start;
    if (arr[middle] < arr[start]) {
        return new Result(new int[]{start, end});
    } else {
        return new Result(middle);
    }
}

public class Result {
    private boolean found;
    private int[] range;
    private int middle;

    public Result(int[] range) {
        this.found = true;
        this.range = range;
    }

    public Result(int middle) {
        this.found = false;
        this.middle = middle;
    }

    public boolean isFound() {
        return found;
    }

    public int[] getRange() {
        return range;
    }

    public int getMiddle() {
        return middle;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int[] arr = new int[2 + new Random().nextInt(50)];
int divideIndex = new Random().nextInt(arr.length);
int dividerTemp = arr.length >> 2;
int temp = 0;
for (int i = 0; i < divideIndex; i++) { // 初始化第 1 个数组
    temp += new Random().nextInt(2);
    if (temp < dividerTemp) {
        temp = dividerTemp;
    }
    arr[i] = temp;
}
temp = 0;
for (int i = divideIndex, size = arr.length; i < size; i++) { // 初始化第 2 个数组
    temp += new Random().nextInt(2);
    if (temp > dividerTemp) {
        temp = dividerTemp;
    }
    arr[i] = temp;
}
System.out.println("arr:" + Arrays.toString(arr));

int min = find(arr);
System.out.println("min:" + min);

时间复杂度：
空间复杂度：

矩阵中的路径

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。

思路：
回溯法。
遍历矩阵，如果矩阵中的某个值和字符串中的第一个值相同，则进入下一级，判断该值在周围四个方向的值和字符串中的下一个值是否相等，如果相等，则继续进入下一级，直到字符串中的值全部找完；否则，回到上一级。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static boolean contains(char[] arr, int rows, int cols, char[] targetArr) {
    boolean[] flagArr = new boolean[arr.length];
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            if (find(arr, flagArr, rows, i, cols, j, targetArr, 0)) {
                return true;
            }
        }
    }
    return false;
}

private static boolean find(char[] arr, boolean[] flagArr, int rows, int rowIndex, int cols, int colIndex, char[] targetArr, int targetIndex) {
    if (rowIndex < 0 || rowIndex > rows - 1) {
        return false;
    }

    if (colIndex < 0 || colIndex > cols - 1) {
        return false;
    }

    int index = rowIndex * cols + colIndex;
    if (flagArr[index] || arr[index] != targetArr[targetIndex]) {
        return false;
    }

    if (targetIndex == targetArr.length - 1) {
        return true;
    }

    flagArr[index] = true;
    if (find(arr, flagArr, rows, rowIndex, cols, colIndex + 1, targetArr, targetIndex + 1)
            || find(arr, flagArr, rows, rowIndex, cols, colIndex - 1, targetArr, targetIndex + 1)
            || find(arr, flagArr, rows, rowIndex + 1, cols, colIndex, targetArr, targetIndex + 1)
            || find(arr, flagArr, rows, rowIndex - 1, cols, colIndex, targetArr, targetIndex + 1)) {
        return true;
    }

    flagArr[index] = false;
    return false;
}
1
2
3
char[] arr = {'a', 'b', 't', 'g', 'c', 'f', 'c', 's', 'j', 'd', 'e', 'h'};
boolean b = contains(arr, 3, 4, new char[]{'b', 'f', 'c', 'e'});
System.out.println("contains:" + b);

时间复杂度：O(n)。
空间复杂度：O(n)。

扩展：打印两个字符间的一条最短路径

思路：
记录水平和竖直方向相对于起点位置的位移。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
public static String findPath(char[] arr, int rows, int cols, char start, char end) {
    boolean[] flagArr = new boolean[arr.length];
    Integer[] stepArr = {0, 0};
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            if (arr[i * cols + j] != start) {
                continue;
            }

            if (findPath(arr, flagArr, rows, i, 0, cols, j, 0, end, stepArr)) {
                StringBuilder builder = new StringBuilder(1 + Math.abs(stepArr[0]) + Math.abs(stepArr[1]));
                builder.append(start);

                if (stepArr[0] > 0) {
                    for (int k = 1, size = stepArr[0]; k <= size; k++) {
                        builder.append(arr[(i + k) * cols + j]);
                    }
                } else {
                    for (int k = -1, size = stepArr[0]; k >= size; k--) {
                        builder.append(arr[(i + k) * cols + j]);
                    }
                }

                if (stepArr[1] > 0) {
                    for (int k = 1, size = stepArr[1]; k <= size; k++) {
                        builder.append(arr[(i + stepArr[0]) * cols + j + k]);
                    }
                } else {
                    for (int k = -1, size = stepArr[1]; k >= size; k--) {
                        builder.append(arr[(i + stepArr[0]) * cols + j + k]);
                    }
                }

                return builder.toString();
            }
        }
    }
    return null;
}

private static boolean findPath(char[] arr, boolean[] flagArr, int rows, int rowIndex, int rowOffset, int cols, int colIndex, int colOffset, char end, Integer[] stepArr) {
    rowIndex += rowOffset;
    colIndex += colOffset;

    if (rowIndex < 0 || rowIndex > rows - 1) {
        return false;
    }

    if (colIndex < 0 || colIndex > cols - 1) {
        return false;
    }

    int index = rowIndex * cols + colIndex;
    if (flagArr[index]) {
        return false;
    }

    if (arr[index] == end) {
        stepArr[0] += rowOffset;
        stepArr[1] += colOffset;
        return true;
    }

    flagArr[index] = true;
    stepArr[0] += rowOffset;
    stepArr[1] += colOffset;
    if (findPath(arr, flagArr, rows, rowIndex, 0, cols, colIndex, 1, end, stepArr)
            || findPath(arr, flagArr, rows, rowIndex, 1, cols, colIndex, 0, end, stepArr)
            || findPath(arr, flagArr, rows, rowIndex, 0, cols, colIndex, -1, end, stepArr)
            || findPath(arr, flagArr, rows, rowIndex, -1, cols, colIndex, 0, end, stepArr)) {
        return true;
    }

    flagArr[index] = false;
    stepArr[0] -= rowOffset;
    stepArr[1] -= colOffset;
    return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int size = 25;
LinkedHashSet<Character> set = new LinkedHashSet<>((int) (size * 1.34));
while (set.size() < size) {
    set.add((char) ('A' + new Random().nextInt(size)));
}

Iterator<Character> iterator = set.iterator();
char[] arr = new char[size];
for (int i = 0; i < size; i++) {
    arr[i] = iterator.next();
}

for (int i = 0; i < 5; i++) {
    StringBuilder builder = new StringBuilder();
    for (int j = 0; j < 5; j++) {
        builder.append(arr[i * 5 + j])
                .append(" ");
    }
    System.out.println(builder.toString());
}

char start = arr[new Random().nextInt(size)];
char end = arr[new Random().nextInt(size)];
String path = findPath(arr, 5, 5, start, end);
System.out.println(start + "->" + end + ":" + path);

机器人的运动范围

地上有一个 m 行 n 列的方格。一个机器人从坐标 (0, 0) 的格子开始移动，它每次可以向左、右、上、下移动一格，但不能进入行坐标和列坐标的数位之和大于 k 的格子。例如，当 k 为 18 时，机器人能够进入方格 (35, 37)，因为 3 + 5 + 3 + 7 = 18。但它不能进入方格 (35, 38)，因为 3 + 5 + 3 + 8 = 19。请问该机器人能够达到多少个格子？

思路：
回溯法。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public static int count(int rows, int cols, int threshold) {
    boolean[][] flagArr = new boolean[rows][cols];
    return count(flagArr, rows, 0, cols, 0, threshold);
}

private static int count(boolean[][] flagArr, int rows, int rowIndex, int cols, int colIndex, int threshold) {
    if (rowIndex < 0 || rowIndex > rows - 1) {
        return 0;
    }

    if (colIndex < 0 || colIndex > cols - 1) {
        return 0;
    }

    if (flagArr[rowIndex][colIndex]) {
        return 0;
    }

    if (!canEnter(rowIndex, colIndex, threshold)) {
        return 0;
    }

    flagArr[rowIndex][colIndex] = true;
    return 1 + count(flagArr, rows, rowIndex, cols, colIndex + 1, threshold)
            + count(flagArr, rows, rowIndex + 1, cols, colIndex, threshold)
            + count(flagArr, rows, rowIndex, cols, colIndex - 1, threshold)
            + count(flagArr, rows, rowIndex - 1, cols, colIndex, threshold);
}

private static boolean canEnter(int row, int col, int threshold) {
    int sum = 0;
    while (row > 0) {
        sum += row % 10;
        row /= 10;
    }
    while (col > 0) {
        sum += col % 10;
        col /= 10;
    }
    return !(sum > threshold);
}
1
2
3
4
5
int m = 10 + new Random().nextInt(10);
int n = 10 + new Random().nextInt(10);
int k = new Random().nextInt(m + n);
int count = count(m, n, k);
System.out.println("m=" + m + "; n=" + n + "; k=" + k + "; count=" + count);

时间复杂度：
空间复杂度：

剪绳子

给你一根长度为 n 的绳子，请把绳子剪成 m 段（m、n 都是整数，n > 1 并且 m > 1），每段绳子的长度记为 k[0]，k[1]，…，k[m]。请问 k[0] x k[1] x … x k[m] 可能的最大乘积是多少？例如，当绳子的长度是 8 时，我们把它剪成长度分别为 2、3、3 的三段，此时得到的最大乘积是 18。

思路：
（1）动态规划法。
任何一根长度为 n 的绳子都可以分为两根长度之和为 n 的绳子，如果其中一根绳子长度为 x，则另一根绳子长度为 n - x。这样，问题就转变为了求两个绳子的问题了，这两根绳子可以再继续一分为二，直至绳子长度为 1，因为 1 分成两个小于 1 的数后，再相乘时值更小。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static long max(int n) throws IllegalArgumentException {
    if (n <= 1) {
        throw new IllegalArgumentException("arg must over 1");
    }

    // 长度 2、3 的绳子不能单独存在，必须至少分出一个 1，然后再计算乘积
    if (n == 2) {
        return 1;
    }
    if (n == 3) {
        return 2;
    }

    long[] maxArr = new long[n + 1];
    // 长度 1、2、3 的绳子作为两段绳子中的一段存在
    maxArr[1] = 1;
    maxArr[2] = 2;
    maxArr[3] = 3;
    for (int i = 4; i <= n; i++) {
        long max = 0;
        for (int j = 1, length = i >> 1; j <= length; j++) {
            long temp = maxArr[j] * maxArr[i - j];
            if (temp < 0) {
                throw new IllegalArgumentException("too big!!!");
            }
            if (temp > max) {
                max = temp;
            }
        }
        maxArr[i] = max;
    }
    System.out.println(Arrays.toString(maxArr));
    return maxArr[n];
}
1
2
int n = new Random().nextInt(100);
System.out.println("n=" + n + "; max:" + max(n));

时间复杂度：O(n^2)。
空间复杂度：O(n)。

扩展：打印剪绳子的具体方案

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public long max(int n) throws IllegalArgumentException {
    if (n <= 1) {
        throw new IllegalArgumentException("arg must over 1");
    }

    // 长度 2、3 的绳子不能单独存在，必须至少分出一个 1，然后再计算乘积
    if (n == 2) {
        return 1;
    }
    if (n == 3) {
        return 2;
    }

    Node[] maxArr = new Node[n + 1];
    // 长度 1、2、3 的绳子作为两段绳子中的一段存在
    maxArr[1] = new Node(1, 1, "1");
    maxArr[2] = new Node(2, 2, "2");
    maxArr[3] = new Node(3, 3, "3");
    for (int i = 4; i <= n; i++) {
        long max = 0;
        for (int j = 1, length = i >> 1; j <= length; j++) {
            long temp = maxArr[j].getValue() * maxArr[i - j].getValue();
            if (temp < 0) {
                throw new IllegalArgumentException("too big!!!");
            }
            if (temp > max) {
                max = temp;
                maxArr[i] = new Node(i, max, maxArr[j].getNote() + " * " + maxArr[i - j].getNote());
            }
        }
    }
    System.out.println(Arrays.toString(maxArr));
    return maxArr[n].getValue();
}

public class Node {
    private int n;
    private long value;
    private String note;

    public Node(int n, long value, String note) {
        this.n = n;
        this.value = value;
        this.note = note;
    }

    public long getValue() {
        return value;
    }

    public String getNote() {
        return note;
    }

    @Override
    public String toString() {
        return "[" + n + "]=" + value + ": " + note + "\n";
    }
}
1
2
int n = new Random().nextInt(100);
System.out.println("n=" + n + "; max:" + max(n));

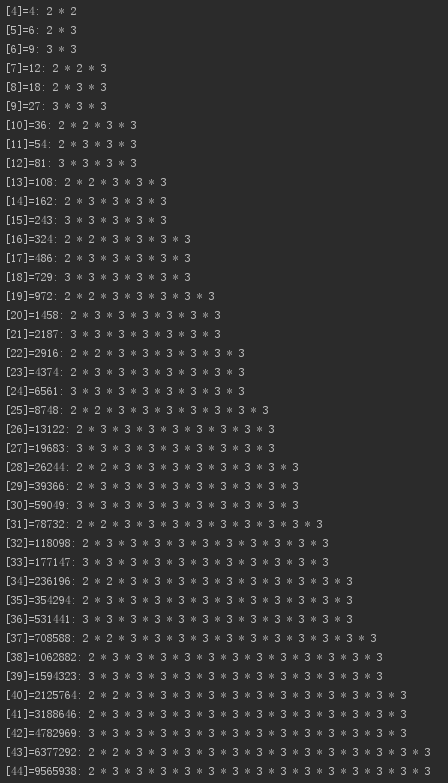
（2）贪婪算法。
根据剪绳子的具体方案可以发现，长度为 n 的绳子，剪成的 m 段绳子，基本是由长度为 2、3 的绳子组成的，比较3 * (n - 3)和2 * (n - 2)，当n >= 5时，3 * (n - 3) >= 2 * (n - 2)，所以当长度大于或等于 5 时，应优先剪 3；否则，剪 2。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static long max(int n) throws IllegalArgumentException {
    if (n <= 1) {
        throw new IllegalArgumentException("arg must over 1");
    }

    // 长度 2、3 的绳子不能单独存在，必须至少分出一个 1，然后再计算乘积
    if (n == 2) {
        return 1;
    }
    if (n == 3) {
        return 2;
    }

    int count = (n >> 1) - (n >> 2);
    int r = n % 3;
    if (r == 2) { // 处理 5
        long sum = 1;
        for (int i = 0; i < count; i++) {
            sum += (sum << 1);
        }
        return sum << 1;
    } else if (r == 1) { // 处理 4
        long sum = 1;
        for (int i = 0; i < count - 1; i++) {
            sum += (sum << 1);
        }
        return sum << 2;
    } else { // 处理 0
        long sum = 1;
        for (int i = 0; i < count; i++) {
            sum += (sum << 1);
        }
        return sum;
    }
}
1
2
int n = new Random().nextInt(100);
System.out.println("n=" + n + "; max:" + max(n));

时间复杂度：O(1)。
空间复杂度：O(1)。

二进制中 1 的个数

请实现一个函数，输入一个整数，输出该数二进制表示中 1 的个数。例如，把 9 表示成二进制是 1001，有 2 位是 1。因此，如果输入 9，则该函数输出 2。

思路：
n & (n - 1)。
（1）当 n 的最右位是 1，n - 1 只是将最右位的 1 变为 0；
（2）当 n 的最右位是 0，n - 1 会先前找 1，找到后将该位置的 1 变为 0，该位置后面全部变为 1，然后变为了（1）；
所以当 n != 0 时，n & (n - 1) 的操作会将最右边的 1 变为 0。

实现：

1
2
3
4
5
6
7
8
public static int count(int n) {
    int count = 0;
    while (n != 0) {
        count++;
        n = n & (n - 1);
    }
    return count;
}
1
2
int n = new Random().nextInt();
System.out.println(n + "=" + Integer.toBinaryString(n) + "b:" + count(n));

时间复杂度：O(n)。
空间复杂度：O(1)。

相关题目：用一条语句判断一个整数是不是 2 的整数次方

思路：
一个整数如果是 2 的整数次方，那么它的二进制表示中有且只有一位是 1，而其他所有位都是 0。

实现：

1
2
3
public static boolean isPow2(int n) {
    return (n & (n - 1)) == 0;
}

相关题目：计算两个数的二进制的不同位的个数

输入两个整数 m 和 n，计算需要改变 m 的二进制表示中的多少位才能得到 n。比如 10 的二进制表示为 1010，13 的二进制表示为 1101，需要改变 1010 中的 3 位才能得到 1101。

思路：
求两个数的异或，统计异或结果中 1 的位数。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int count(int m, int n) {
    int i = m ^ n;
    System.out.println(m + "^" + n + "=" + Integer.toBinaryString(i) + "b");
    return count(i);
}


private static int count(int n) {
    int count = 0;
    while (n != 0) {
        count++;
        n = n & (n - 1);
    }
    return count;
}
1
2
3
4
5
int m = new Random().nextInt();
int n = new Random().nextInt();
System.out.println(m + "=" + Integer.toBinaryString(m) + "b");
System.out.println(n + "=" + Integer.toBinaryString(n) + "b");
System.out.println("count:" + count(m, n));

数值的整数次方

实现函数 double Power(double base, int exponent)，求 base 的 exponent 次方。不得使用库函数，同时不需要考虑大数问题。已知公式：

思路：
（1）当 base == 0 时，函数返回 0；
（2）当 exponent == 0 时，函数返回 1；
（3）当 exponent < 0 时，base = 1 / base，exponent = -exponent；
（4）利用提供的公式计算。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static double Power(double base, int exponent) {
    if (base == 0) {
        return 0;
    }

    if (exponent == 0) {
        return 1;
    }

    if (exponent < 0) {
        base = 1 / base;
        exponent = -exponent;
    }

    return cal(base, exponent);
}

private static double cal(double base, int exponent) {
    if (exponent == 0) {
        return 1;
    }

    double result;
    if ((exponent & 1) == 0) {// n 为偶数
        exponent = exponent >> 1;
        result = cal(base, exponent);
        result *= result;
    } else {// n 为奇数
        exponent = (exponent - 1) >> 1;
        result = cal(base, exponent);
        result *= result;
        result *= base;
    }
    return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int base = new Random().nextInt();
if (base > 8) {
    base &= 7;
} else if (base < -8) {
    base &= 7;
    base = -base;
}
int exponent = new Random().nextInt();
if (exponent > 8) {
    exponent &= 7;
} else if (exponent < -8) {
    exponent &= 7;
    exponent = -exponent;
}
System.out.println("base=" + base);
System.out.println("exponent=" + exponent);
System.out.println("Power:" + Power(base, exponent));

时间复杂度：O(logn)。
空间复杂度：O(logn)。

打印从 1 到最大的 n 位数

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

思路：
考虑大数问题，不能直接打印。
（1）输入数字 <= 0 时，不打印；
（2）输入数字 > 0 时，递归调用位数少 1 位的方法，直到调用到位数为 1 的方法后开始打印。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public static void print(int count) {
    print("", count);
}

private static void print(String pre, int count) {
    if (count < 1) {
        return;
    }

    if (count != 1) {
        if (pre.length() > 0) { // 针对于 3 位数及以上
            print(pre + "0", count - 1);
        } else { // 针对于 2 位数
            print(pre, count - 1);
        }
        for (int i = 1; i <= 9; i++) {
            print(pre + i, count - 1);
        }
    } else {
        for (int i = 0; i <= 9; i++) {
            System.out.println(pre + i);
        }
    }
}
1
2
3
int n = new Random().nextInt();
System.out.println("print(" + n + "):\n");
print(n);

时间复杂度：
空间复杂度：O(n)。

扩展：实现任意两个整数的加（减）法

思路：
（1）两个正整数相加时，结果的位数最多比这两个数中最大值的位数多 1 位。按照小学加法，以递归方式依次从最低位开始加，是否有进位也需要带到下一次计算中；
（2）两个正整数相减时，需要先确定两个数中哪个更大，确保让大数减小数。结果的位数最多为这两个数中最大值的位数，计算以递归方式依次从最低位开始减，低位向高位借 1 时直接在高位减 1；
（2）当两个值中有负整数时，通过截取字符串变为正整数，同时转变为等价的运算。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
public static String sub(String value1, String value2) {
    boolean value1IsNeg = '-' == value1.charAt(0);
    boolean value2IsNeg = '-' == value2.charAt(0);
    if (value1IsNeg && value2IsNeg) {
        return sub(value2.substring(1), value1.substring(1));
    } else if (!value1IsNeg && value2IsNeg) {
        return add(value1, value2.substring(1));
    } else if (value1IsNeg) {
        return "-" + add(value1.substring(1), value2);
    }

    boolean value1IsLarger = true;
    if (value2.length() > value1.length()) {
        value1IsLarger = false;
    } else if (value2.length() == value1.length()) {
        if (Integer.parseInt(String.valueOf(value2.charAt(0))) > Integer.parseInt(String.valueOf(value1.charAt(0)))) {
            value1IsLarger = false;
        }
    }

    Integer[] arr1 = convertArray2(value1);
    Integer[] arr2 = convertArray2(value2);
    Integer[] arr = new Integer[Math.max(arr1.length, arr2.length)];
    StringBuilder builder = new StringBuilder(arr.length);
    if (value1IsLarger) {
        sub(arr1, arr2, arr, 0);
    } else {
        sub(arr2, arr1, arr, 0);
        builder.append("-");
    }

    for (int i = 0; i < arr.length; i++) {
        Integer integer = arr[i];
        if (i == 0 && integer == 0) {
            continue;
        }
        builder.append(integer);
    }
    return builder.toString();
}

private static void sub(Integer[] arr1, Integer[] arr2, Integer[] arr, int lastIndex) {
    if (lastIndex == arr.length) {
        return;
    }

    int arr1Index = arr1.length - 1 - lastIndex;
    int arr2Index = arr2.length - 1 - lastIndex;
    // arr1 和 arr2 位数相同，且都算到了最高位的前一位
    if (arr1Index < 0 && arr2Index < 0) {
        return;
    }

    // arr2 算到了最高位的前一位，后续计算只和 arr1 有关，执行快速计算
    if (arr2Index < 0) {
        fastSub(arr1, arr, arr1Index);
        return;
    }

    // arr1 和 arr2 都没有算到最高位的前一位
    // （1）先计算当前位
    int value = arr1[arr1Index] - arr2[arr2Index];
    if (value < 0) {
        borrow(arr1, arr1Index - 1);
        arr[arr.length - 1 - lastIndex] = value + 10;
    } else {
        arr[arr.length - 1 - lastIndex] = value;
    }
    // （2）计算前一位
    sub(arr1, arr2, arr, ++lastIndex);
}

private static void fastSub(Integer[] arr1, Integer[] arr, int arr1Index) {
    System.arraycopy(arr1, 0, arr, 0, arr1Index + 1);
}

private static void borrow(Integer[] arr, int lastIndex) {
    for (int i = lastIndex; i >= 0; i--) {
        if (arr[i] > 0) {
            arr[i]--;
            return;
        }
    }
}

public static String add(String value1, String value2) {
    boolean value1IsNeg = '-' == value1.charAt(0);
    boolean value2IsNeg = '-' == value2.charAt(0);
    if (value1IsNeg && value2IsNeg) {
        return "-" + add(value2.substring(1), value1.substring(1));
    } else if (!value1IsNeg && value2IsNeg) {
        return sub(value1, value2.substring(1));
    } else if (value1IsNeg) {
        return sub(value2, value1.substring(1));
    }

    int[] arr1 = convertArray(value1);
    int[] arr2 = convertArray(value2);
    Integer[] arr = new Integer[Math.max(arr1.length, arr2.length) + 1];
    add(arr1, arr2, arr, 0, false);

    StringBuilder builder = new StringBuilder(arr.length);
    for (int i = 0; i < arr.length; i++) {
        if (i == 0) {
            if (arr[i] != 0) {
                builder.append(arr[i]);
            }
        } else {
            builder.append(arr[i]);
        }
    }
    return builder.toString();
}

private static void add(int[] arr1, int[] arr2, Integer[] arr, int lastIndex, boolean carry) {
    if (lastIndex == arr.length) {
        return;
    }

    int arr1Index = arr1.length - 1 - lastIndex;
    int arr2Index = arr2.length - 1 - lastIndex;
    // arr1 和 arr2 位数相同，且都算到了最高位的前一位
    if (arr1Index < 0 && arr2Index < 0) {
        if (carry) {
            arr[0] = 1;
        } else {
            arr[0] = 0;
        }
        return;
    }

    // arr1 算到了最高位的前一位，后续计算只和 arr2 有关，执行快速计算
    if (arr1Index < 0) {
        fastAdd(arr2, arr, arr2Index, carry);
        return;
    }

    // arr2 算到了最高位的前一位，后续计算只和 arr1 有关，执行快速计算
    if (arr2Index < 0) {
        fastAdd(arr1, arr, arr1Index, carry);
        return;
    }

    // arr1 和 arr2 都没有算到最高位的前一位
    // （1）先计算当前位
    int value = arr1[arr1Index] + arr2[arr2Index];
    if (carry) {
        value++;
    }
    if (value > 9) {
        arr[arr.length - 1 - lastIndex] = value - 10;
        carry = true;
    } else {
        arr[arr.length - 1 - lastIndex] = value;
        carry = false;
    }
    // （2）计算前一位
    add(arr1, arr2, arr, ++lastIndex, carry);
}

private static void fastAdd(int[] arr1, Integer[] arr, int arr1Index, boolean carry) {
    // arr 位数比 arr1 位数多 1 位，多的是最高位
    // （1）先计算当前位和前一位（或前 n 位）
    int value = arr1[arr1Index];
    if (carry) {
        value++;
    }
    if (value > 9) {
        arr[arr1Index + 1] = value - 10;
        // 如果当前位已经是 arr1 的最高位，则直接可以确定 arr[0] 并返回
        if (arr1Index == 0) {
            arr[0] = 1;
            return;
        } else {
            // 否则，计算前一位（如果前一位加 1 后正好进位，则继续计算前一位）
            while (arr1[arr1Index - 1] == 9) {
                arr[arr1Index] = 0;
                arr1Index--;
                if (arr1Index == 0) {
                    arr[0] = 1;
                    return;
                }
            }
            // 再计算前一位 ，此时加 1 必小于 10
            arr[arr1Index] = arr1[arr1Index - 1] + 1;
            // 如果当前位是 arr1 的次高位，则直接可以确定 arr[0] 并返回
            if (arr1Index == 1) {
                arr[0] = 0;
                return;
            }
        }
    } else {
        arr[arr1Index + 1] = value;
        // 如果当前位已经是 arr1 的最高位，则直接可以确定 arr[0] 并返回
        if (arr1Index == 0) {
            arr[0] = 0;
            return;
        } else {
            // 否则，计算前一位
            arr[arr1Index] = arr1[arr1Index - 1];
            // 如果当前位是 arr1 的次高位，则直接可以确定 arr[0] 并返回
            if (arr1Index == 1) {
                arr[0] = 0;
                return;
            }
        }
    }

    // （2）将 arr1[0]~arr1[arr1Index - 2] 复制给 arr[1]~arr1[arr1Index - 1]
    for (int i = 0, size = arr1Index - 1; i < size; i++) {
        arr[i + 1] = arr1[i];
    }
    // （3）arr[0]
    arr[0] = 0;
}

private static int[] convertArray(String str) {
    int[] arr = new int[str.length()];
    for (int i = 0, size = str.length(); i < size; i++) {
        arr[i] = Integer.parseInt(String.valueOf(str.charAt(i)));
    }
    return arr;
}

private static Integer[] convertArray2(String str) {
    Integer[] arr = new Integer[str.length()];
    for (int i = 0, size = str.length(); i < size; i++) {
        arr[i] = Integer.parseInt(String.valueOf(str.charAt(i)));
    }
    return arr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int mLen = new Random().nextInt(6);
String m;
StringBuilder builder = new StringBuilder(mLen + 1);
builder.append(1 + new Random().nextInt(9));
for (int i = 1; i < mLen; i++) {
    builder.append(new Random().nextInt(10));
}
if (new Random().nextInt(2) == 0) {
    builder.insert(0, "-");
}
m = builder.toString();

int nLen = new Random().nextInt(6);
String n;
builder = new StringBuilder(nLen + 1);
builder.append(1 + new Random().nextInt(9));
for (int i = 1; i < nLen; i++) {
    builder.append(new Random().nextInt(10));
}
if (new Random().nextInt(2) == 0) {
    builder.insert(0, "-");
}
n = builder.toString();

System.out.println("m=" + m + "; n=" + n);
System.out.println("add:" + add(m, n));
System.out.println("sub:" + sub(m, n));

删除链表的节点

题目一：在 O(1) 时间内删除链表节点

给定单向链表的头指针和一个节点指针，定义一个函数在 O(1) 时间内删除该节点。

思路：
（1）对于头节点，直接将头节点指向下一个节点；
（2）对于尾节点，从头遍历找到前一个节点，将该节点的下一个节点置为 null；
（3）对于中间的节点，将要删除的节点的信息修改成下一个节点的信息，本质是删除了下一个节点。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
public static Node remove(Node firstNode, Node deleteNode) {
    // 删除头节点
    if (firstNode.equals(deleteNode)) {
        return deleteNode;
    }

    Node tempNode = firstNode;
    while (tempNode.hasNext()) {
        tempNode = tempNode.getNext();
        if (tempNode.equals(deleteNode)) {
            Node nextNode = deleteNode.getNext();
            // 删除的节点不是尾节点，复制后一个节点的信息给要删除的节点
            if (nextNode != null) {
                tempNode.setValue(nextNode.getValue());
                tempNode.setNext(nextNode.getNext());
                return deleteNode;
            }

            // 删除的节点是尾节点，需要找到前一个节点
            Node beforeNode;
            tempNode = firstNode;
            while (tempNode.hasNext()) {
                beforeNode = tempNode;
                tempNode = tempNode.getNext();
                if (tempNode.equals(deleteNode)) {
                    beforeNode.setNext(null);
                    return deleteNode;
                }
            }
        }
    }
    return null;
}

private Node createNode(int index, int count) {
    if (index < count) {
        Node node = createNode(index + 1, count);
        return new Node(index, node);
    }
    return new Node(index, null);
}

public class Node {
    private int value;
    private Node next;

    public Node(int value, Node next) {
        this.value = value;
        this.next = next;
    }

    public Node getNext() {
        return this.next;
    }

    public void setNext(Node next) {
        this.next = next;
    }

    public int getValue() {
        return this.value;
    }

    public void setValue(int value) {
        this.value = value;
    }

    public boolean hasNext() {
        return next != null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int count = 1 + new Random().nextInt(10);
Node firstNode = createNode(0, count - 1);

int delete = new Random().nextInt(count);
Node deleteNode = firstNode;
for (int i = 0; i < delete; i++) {
    deleteNode = deleteNode.getNext();
}

System.out.println("deleteNode:" + deleteNode.getValue());
Node node = firstNode;
System.out.println("node:" + node.getValue());
while (node.hasNext()) {
    node = node.getNext();
    System.out.println("node:" + node.getValue());
}
System.out.println("---");

Node removeNode = remove(firstNode, deleteNode);
if (firstNode.equals(removeNode)) {
    firstNode = firstNode.getNext();
}

node = firstNode;
if (node != null) {
    System.out.println("node:" + node.getValue());
    while (node.hasNext()) {
        node = node.getNext();
        System.out.println("node:" + node.getValue());
    }
}

时间复杂度：O(1)。对于 n 个节点的链表，只有尾节点是 O(n)，其余节点都是 O(1)。
空间复杂度：O(1)。

题目二：删除链表中重复的节点

在一个排序的链表中，如何删除重复的节点？

思路：
定义 3 个指针，分别指向已确定的节点（beforeNode），当前需要判断的节点（currentNode）及其下一个节点（afterNode）。为了防止头节点就是需要删除的重复节点，在头节点前构造一个不重复的节点，最后再将头节点指向该节点的下一个节点。
遍历节点，当 currentNode 和 afterNode 值不相等时，将 currentNode 放到 beforeNode 后，否则，记录这个值，再往后遍历，直到找到不等于这个值的节点，如果这个节点是尾节点，则直接将这个节点放到 beforeNode 后；否则将这个节点作为 currentNode，继续判断 currentNode 和 afterNode 值是否相等。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public static void remove(Node firstNode) {
    Node beforeNode = firstNode;
    Node currentNode = firstNode.getNext();
    Node afterNode;
    while (currentNode != null && currentNode.hasNext()) {
        afterNode = currentNode.getNext();
        if (afterNode == null
                || currentNode.getValue() != afterNode.getValue()) {
            beforeNode.setNext(currentNode);
            beforeNode = currentNode;
            currentNode = afterNode;
        } else {
            beforeNode.setNext(null);
            int value = currentNode.getValue();
            while (currentNode.hasNext()) {
                currentNode = currentNode.getNext();
                if (currentNode.getValue() != value) {
                    if (!currentNode.hasNext()) {
                        beforeNode.setNext(currentNode);
                    } else {
                        break;
                    }
                }
            }
        }
    }
}

private Node createNode(int index, int max) {
    if (index < max) {
        int random = new Random().nextInt(2);
        Node node = createNode(index + random, max);
        return new Node(index, node);
    }
    return new Node(index, null);
}

public class Node {
    private int value;
    private Node next;

    public Node(int value, Node next) {
        this.value = value;
        this.next = next;
    }

    public Node getNext() {
        return this.next;
    }

    public void setNext(Node next) {
        this.next = next;
    }

    public int getValue() {
        return this.value;
    }

    public boolean hasNext() {
        return next != null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int max = 1 + new Random().nextInt(10);
Node firstNode = createNode(0, max);

Node node = firstNode;
System.out.println("node:" + node.getValue());
while (node.hasNext()) {
    node = node.getNext();
    System.out.println("node:" + node.getValue());
}
System.out.println("---");

Node toolNode = new Node(firstNode.getValue() - 1, firstNode);
remove(toolNode);

node = toolNode.getNext();
if (node != null) {
    System.out.println("node:" + node.getValue());
    while (node.hasNext()) {
        node = node.getNext();
        System.out.println("node:" + node.getValue());
    }
}

时间复杂度：
空间复杂度：

正则表达式匹配

请实现一个函数用来匹配包含’.‘和’*‘的正则表达式。模式中的字符’.‘表示任意一个字符，而’*'表示它前面的字符可以出现任意次（含 0 次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串"aaa"与模式"a.a"和"abaca"匹配，但与"aa.a"和“ab*a”均不匹配。

思路：
取模式串的前两个字符和字符串的一个字符——
（1）处理’*‘。如果模式串的第 2 个字符是’*‘，则从字符串的字符向后遍历，直到字符串的字符和模式串的第 1 个字符不相等，从这个位置开始后面的匹配；
（2）处理’.‘。因为’.'表示任意一个字符，所以直接从下一个字符开始匹配；
（3）判断模式串和字符串的一个字符是否相等。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static boolean match(String regex, String str) {
    char[] regexArr = regex.toCharArray();
    char[] arr = str.toCharArray();
    return match(regexArr, 0, arr, 0);
}

private static boolean match(char[] regexArr, int regexArrIndex, char[] arr, int arrIndex) {
    if (regexArrIndex == regexArr.length && arrIndex == arr.length) {
        return true;
    }

    if (regexArrIndex == regexArr.length || arrIndex == arr.length) {
        return false;
    }

    char cRegex = regexArr[regexArrIndex];
    char aRegex = ' ';
    if (regexArrIndex < regexArr.length - 1) {
        aRegex = regexArr[regexArrIndex + 1];
    }

    if (aRegex == '*') {
        while (arr[arrIndex] == cRegex) {
            arrIndex++;
        }
        return match(regexArr, regexArrIndex + 2, arr, arrIndex);
    } else {
        if (cRegex == '.' || arr[arrIndex] == cRegex) {
            return match(regexArr, regexArrIndex + 1, arr, arrIndex + 1);
        } else {
            return false;
        }
    }
}
1
2
3
4
System.out.println("match:" + match("a.a", "aaa"));
System.out.println("match:" + match("ab*ac*a", "aaa"));
System.out.println("match:" + match("aa.a", "aaa"));
System.out.println("match:" + match("ab*a", "aaa"));

时间复杂度：O(n)。
空间复杂度：O(n)。

表示数值的字符串

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串"+100"、“5e2”、“-123”、“3.1416"及”-1E-16"都表示数值，但"12e"、“1a3.14”、“1.2.3”、"±5"及"12e+5.4"都不是。

思路：
‘e’、‘E’后面必须有数字，数字之间不能有’.'；
字符可以是[0-9]、‘e’、‘E’；
‘e’或’E’之前的’.‘最多只能有一个；
‘+’、’-'开头时，只能有一个；
（例子中未完全体现限制，还需要根据常识补充）。

实现：
略。

时间复杂度：
空间复杂度：

《剑指 Offer》算法题（20/68）
https://weichao.io/de67cf472b53/
作者
魏超
发布于
2020年3月23日
更新于
2022年12月4日
许可协议