《剑指 Offer》算法题（10/68）

本文最后更新于：1 年前

Reference

赋值运算符函数

Java 不支持用户自定义操作符重载。

实现 Singleton 模式

设计一个类，我们只能生成该类的一个实例。

饿汉式

1
2
3
4
5
6
7
8
9
public class SingleTon{
	private static SingleTon mSingleTon = new SingleTon();
	
	private SingleTon() {}
	
	public static SingleTon getInstance() {
		return mSingleTon;
	}
}

懒汉式(线程不安全)

1
2
3
4
5
6
7
8
9
10
11
12
public class SingleTon{
	private static SingleTon mSingleTon = null;
	
	private SingleTon() {}
	
	public static SingleTon getInstance() {
		if(mSingleTon == null) {
			mSingleTon = new SingleTon();
		}
		return mSingleTon;
	}
}

懒汉式(线程安全)

1
2
3
4
5
6
7
8
9
10
11
12
public class SingleTon{
	private static SingleTon mSingleTon = null;
	
	private SingleTon() {}
	
	public static synchronized SingleTon getInstance() {
		if(mSingleTon == null) {
			mSingleTon = new SingleTon();
		}
		return mSingleTon;
	}
}

懒汉式(双重校验锁，线程不一定安全)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class SingleTon{
	private static SingleTon mSingleTon = null;
	
	private SingleTon() {}
	
	public static SingleTon getInstance() {
		if(mSingleTon == null){
			synchronized(SingleTon.class) {
				if(mSingleTon == null) {
					mSingleTon = new SingleTon();
				}
			}
		}
		return mSingleTon;
	}
}

懒汉式(双重校验锁，线程安全)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class SingleTon{
	private static volatile SingleTon mSingleTon = null;
	
	private SingleTon() {}
	
	public static SingleTon getInstance() {
		if(mSingleTon == null){
			synchronized(SingleTon.class) {
				if(mSingleTon == null) {
					mSingleTon = new SingleTon();
				}
			}
		}
		return mSingleTon;
	}
}

枚举

1
2
3
4
5
enum SingleTon {
	SINGLE
}

SingleTon.SINGLE

静态内部类

1
2
3
4
5
6
7
8
9
10
11
public class SingleTon {
	private static class InnerClass {
		static SingleTon mSingleTon = new SingleTon();
	}
	
	private SingleTon() {}
	
	public static SingleTon getInstance() {
		return InnerClass.mSingleTon;
	}
}

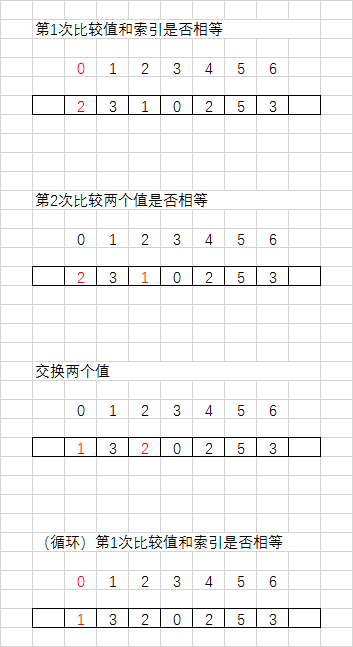
数组中重复的数字

找出数组中重复的数字

在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了。也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。例如，如果输入长度为 7 的数组 {2, 3, 1, 0, 2, 5, 3}，那么对应的输出是重复的数字 2 或者 3。

思路：
观察值的范围，当数组中没有重复数字时，排序之后的结果应该是值和索引一一对应。以此为突破口，尝试给数组排序。
遍历数组，当值和索引相等时，继续处理下个索引的值；否则，比较当前值（arr[i] == m）和值作为索引的值（arr[m]），如果相等则说明找到了重复的数字，否则，交换两个值，再执行该过程。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public static int find(int[] arr) {
    for (int i = 0, size = arr.length; i < size; i++) {
        while (arr[i] != i) {
            if (arr[i] == arr[arr[i]]) {
                return arr[i];
            }

            int temp = arr[i];
            arr[i] = arr[temp];
            arr[temp] = temp;
        }
    }

    return -1;
}
1
2
3
int[] arr = {2, 3, 1, 0, 2, 5, 3};
int value = find(arr);
System.out.println("value:" + value);

时间复杂度：O(n)。代码中尽管有一个两重循环，但每个数字最多只要交换两次就能找到位置。
空间复杂度：O(1)。所有操作都是在输入数组上进行，不需要额外分配内存。

不修改数组找出重复的数字

在一个长度为 n + 1 的数组里的所有数字都在 1 到 n 的范围内，所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字，但不能修改输入的数组。例如，如果输入长度为 8 的数组 {2, 3, 5, 4, 3, 2, 6, 7}，那么对应的输出是重复的数字 2 或者 3。

思路：
将值按照大于 m 值的和不大于 m 值的分为大、小两个区间，数组如果不重复（n 个元素对应 1~n），则大区间中必有 m 个元素，且小区间中必有 n - m 个元素，但是由于多 1 个元素，所以至少有大区间元素个数大于 m，或小区间元素个数大于 m - n。以此为突破口，统计数组在各区间元素的个数。
遍历数组，找到元素个数大于区间的，将该区间重新划分大、小两个区间；重复此步骤，直至区间不可再划分。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public static int find(int[] arr) {
    int start = 1;
    int end = arr.length - 1;
    while (end >= start) {
        int middle = ((end - start) >> 1) + start;
        int count = count(arr, start, middle);
        if (start == middle) {
            if (count > 1) {
                return start;
            } else {
                break;
            }
        }

        if (count > middle - start + 1) {
            end = middle;
        } else {
            start = middle + 1;
        }
    }
    return -1;
}

private static int count(int[] arr, int start, int middle) {
    int count = 0;
    for (int i : arr) {
        if (i >= start && i <= middle) {
            count++;
        }
    }
    return count;
}
1
2
3
int[] arr = {2, 3, 5, 4, 3, 2, 6, 7};
int value = find(arr);
System.out.println("value:" + value);

时间复杂度：O(nlogn)。数组长度为 n，是 O(n)，二分查找是 O(logn)，所以总时间是 O(nlogn)。
空间复杂度：O(1)。

二维数组中的查找

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

思路：
二维数组行、列都是有序的，所以如果列的第一个元素大于目标值时，则目标值不可能在此列；同理，行也一样。以此为突破口，先用二分法缩小目标可能存在的范围，再遍历。
使用二分法找到中间列，判断列的第一个元素和目标值的大小关系，如果等于，说明找到了，直接返回；如果大于，记录位置为 C1；如果小于，记录位置为 C2。重复此过程，直到 C2 >= C1，则找到了列在遍历时的最大值 C2 - 1。同理，再找到行在遍历时的最大值。然后从列的最大值开始遍历，查找目标值。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public static boolean contain(int[][] arr, int target) {
    int maxCol = findMaxCol(arr, target);
    if (arr[0][maxCol] == target) {
        return true;
    }

    int maxRow = findMaxRow(arr, target);
    if (arr[maxRow][0] == target) {
        return true;
    }

    for (int j = maxCol; j >= 0; j--) {
        for (int i = maxCol - j; i <= maxRow; i++) {
            if (arr[i][j] == target) {
                return true;
            } else if (arr[i][j] > target) {
                break;
            }
        }
    }
    return false;
}

private static int findMaxCol(int[][] arr, int target) {
    int start = 0;
    int end = arr[0].length - 1;
    while (end >= start) {
        int middle = ((end - start) >> 1) + start;
        if (arr[0][middle] == target) {
            return middle;
        } else if (arr[0][middle] > target) {
            end = middle - 1;
        } else {
            start = middle + 1;
        }
    }
    return start - 1;
}

private static int findMaxRow(int[][] arr, int target) {
    int start = 0;
    int end = arr.length - 1;
    while (end >= start) {
        int middle = ((end - start) >> 1) + start;
        if (arr[middle][0] == target) {
            return middle;
        } else if (arr[middle][0] > target) {
            end = middle - 1;
        } else {
            start = middle + 1;
        }
    }
    return start - 1;
}
1
2
3
int[][] arr = {{1, 2, 8, 9}, {2, 4, 9, 12}, {4, 7, 10, 13}, {6, 8, 11, 15}};
boolean b = contain(arr, 7);
System.out.println("contain:" + b);

时间复杂度：
空间复杂度：O(1)。

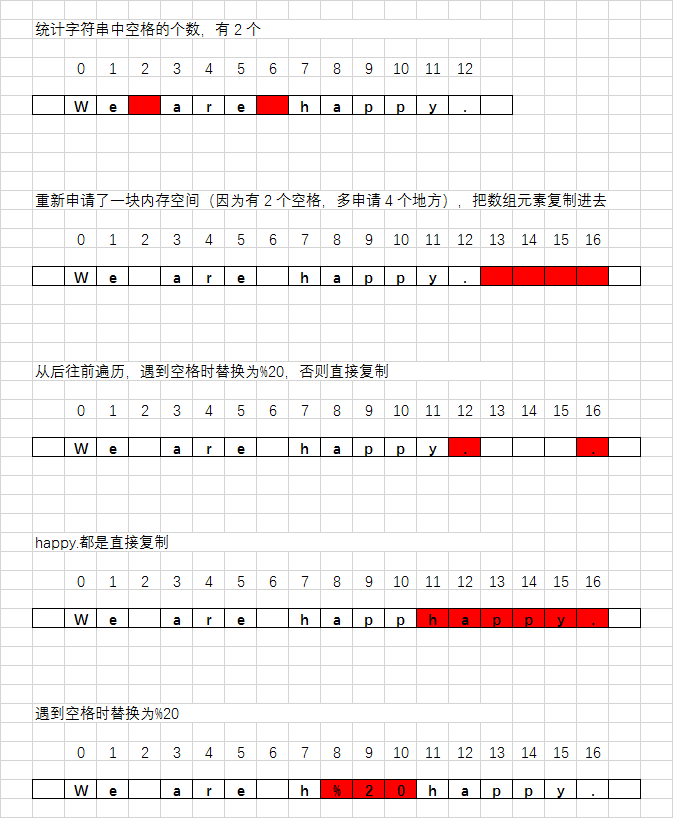
替换空格

请实现一个函数，把字符串中的每个空格替换成"%20"。例如，输入"We are happy.“，则输出"We%20are%20happy.”。

思路：
操作同一个数组时，如果从前往后替换会导致后面的数据被覆盖。因为每替换 1 个空格，数组所需的长度需要 + 2，所以可以以此为突破口，从后往前替换。
统计字符串中空格的个数，先计算出替换后的长度，由于 Java 数组长度不可变，所以以计算出的长度重新申请一块内存，然后再从后往前遍历，遇到空格时替换为%20，否则直接复制。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static void convert(StringBuffer stringBuffer) {
    int count = 0;
    for (int i = 0, size = stringBuffer.length(); i < size; i++) {
        if (stringBuffer.charAt(i) == ' ') {
            count++;
        }
    }

    int oldLen = stringBuffer.length();
    int newLen = oldLen + (count << 1);
    stringBuffer.setLength(newLen);
    for (int i = oldLen - 1, j = newLen - 1; i >= 0; i--, j--) {
        char c = stringBuffer.charAt(i);
        if (c == ' ') {
            stringBuffer.setCharAt(j, '0');
            stringBuffer.setCharAt(--j, '2');
            stringBuffer.setCharAt(--j, '%');
        } else {
            stringBuffer.setCharAt(j, c);
        }
    }
}
1
2
3
4
StringBuffer stringBuffer = new StringBuffer("We are happy.");
System.out.println("stringBuffer:" + stringBuffer.toString());
convert(stringBuffer);
System.out.println("stringBuffer:" + stringBuffer.toString());

时间复杂度：O(n)。
空间复杂度：O(n)。

相关题目：把数组 A2 中的所有数字插入数组 A1 中

有两个排序的数组 A1 和 A2，内存在 A1 的末尾有足够多的空余空间容纳 A2。请实现一个函数，把 A2 中的所有数字插入 A1 中，并且所有的数字是排序的。

思路：
合并两个数组，可以知道两个数组占用的总的空间大小。以此为突破口，合并数组 A2 到 A1。
计算总大小，比较数组 A1 和 A2 各自最后位置的元素的大小，将更大的元素放到末尾。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 随机初始化数组中的元素
int[] arr1src = new int[10];
int[] arr2 = new int[10];
int beforeValue = 0;
for (int i = 0, size = arr1src.length; i < size; i++) {
    int random = new Random().nextInt(10);
    beforeValue += random;
    arr1src[i] = beforeValue;
}
beforeValue = 0;
for (int i = 0, size = arr2.length; i < size; i++) {
    int random = new Random().nextInt(10);
    beforeValue += random;
    arr2[i] = beforeValue;
}

int[] arr1 = new int[100];
System.arraycopy(arr1src, 0, arr1, 0, arr1src.length); // 由于 Java 中数组长度不可变，此处假装数组 A1 末尾有足够多的空余空间
System.out.println("arr1:" + Arrays.toString(arr1));
System.out.println("arr2:" + Arrays.toString(arr2));

int i = arr1src.length - 1, j = arr2.length - 1, index = arr1src.length + arr2.length - 1;
while (i >= 0 && j >= 0) {
    int v1 = arr1[i];
    int v2 = arr2[j];
    if (v1 == v2) {
        arr1[index--] = v1;
        arr1[index--] = v2;
        i--;
        j--;
    } else if (v1 > v2) {
        arr1[index--] = v1;
        i--;
    } else {
        arr1[index--] = v2;
        j--;
    }
}
if (j >= 0) { // 最小值在 A2 数组时，直接把剩余元素复制到 A1 数组开头
    System.arraycopy(arr2, 0, arr1, 0, j + 1);
}
System.out.println("arr1:" + Arrays.toString(arr1));

时间复杂度：O(n)。
空间复杂度：O(1)。

从尾到头打印链表

输入一个链表的头节点，从尾到头反过来打印出每个节点的值。

思路：
判断单向链表中的节点，如果持有节点为空，则说明不是该节点是尾节点，可以打印了；否则可以继续判断持有的节点是否还持有节点。循环此过程。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class Node {
    private int value;
    private Node next;

    public Node(int value, Node next) {
        this.value = value;
        this.next = next;
    }

    public Node getNext() {
        return this.next;
    }

    public int getValue() {
        return this.value;
    }
}

public static void print(Node node) {
    if (node.getNext() != null) {
        print(node.getNext());
    }
    System.out.println("value:" + node.getValue());
}
1
2
3
4
5
6
7
8
9
10
11
12
13
Node node = null;
for (int i = 10; i > 0; i--) {
    node = new Node(i, node);
}

Node firstNode = node;

while (node != null) {
    System.out.println("value:" + node.getValue());
    node = node.getNext();
}

print(firstNode);

时间复杂度：O(n)。
空间复杂度：O(1)。

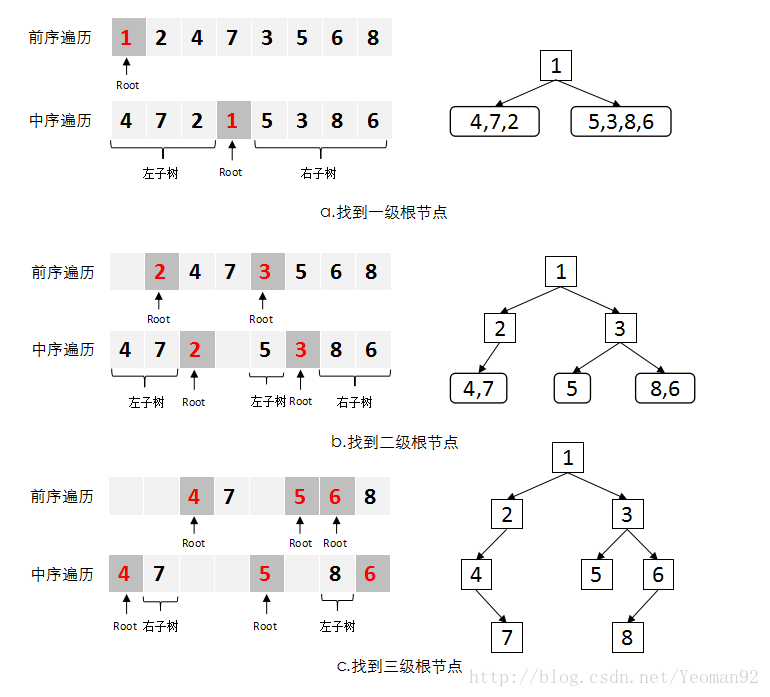
重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1, 2, 4, 7, 3, 5, 6, 8}和中序遍历序列{4, 7, 2, 1, 5, 3, 8, 6}，则重建二叉树并输出它的头节点。

思路：

（1）前序遍历看根节点；
（2）中序遍历看左子树、右子树；
（3）把子树值带回前序遍历，排在前面的是根节点；
（4）重复（2）（3）过程，直到左子树、右子树为空。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class Node {
    private int value;
    private Node left;
    private Node right;

    public Node(int value) {
        this.value = value;
    }

    public int getValue() {
        return this.value;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }
}

public Node create(int[] preorderArr, int[] inorderArr) {
    if (preorderArr == null || preorderArr.length == 0 ||
            inorderArr == null || inorderArr.length == 0) {
        return null;
    }

    Node node = new Node(preorderArr[0]);
    for (int i = 0, size = inorderArr.length; i < size; i++) {
        if (preorderArr[0] == inorderArr[i]) { // 根节点
            node.setLeft(create(Arrays.copyOfRange(preorderArr, 1, i + 1), Arrays.copyOfRange(inorderArr, 0, i)));
            node.setRight(create(Arrays.copyOfRange(preorderArr, i + 1, preorderArr.length), Arrays.copyOfRange(inorderArr, i + 1, inorderArr.length)));
        }
    }
    return node;
}
1
2
3
4
5
int[] preorderArr = {1, 2, 4, 7, 3, 5, 6, 8};
int[] inorderArr = {4, 7, 2, 1, 5, 3, 8, 6};

Node node = create(preorderArr, inorderArr);
System.out.println("node:" + node.getValue());

时间复杂度：O(nlogn)。
空间复杂度：O(n)。

扩展：输入某二叉树的中序遍历和后序遍历的结果，重建出该二叉树

思路：
（1）后序遍历看根节点；
（2）中序遍历看左子树、右子树；
（3）把子树值带回后序遍历，排在前面的是根节点；
（4）重复（2）（3）过程，直到左子树、右子树为空。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private Node create(int[] inorderArr, int[] postorderArr) {
    if (inorderArr == null || inorderArr.length == 0 ||
            postorderArr == null || postorderArr.length == 0) {
        return null;
    }

    Node node = new Node(postorderArr[postorderArr.length - 1]);
    for (int i = 0, size = inorderArr.length; i < size; i++) {
        if (postorderArr[postorderArr.length - 1] == inorderArr[i]) { // 根节点
            node.setLeft(create(Arrays.copyOfRange(inorderArr, 0, i), Arrays.copyOfRange(postorderArr, 0, i)));
            node.setRight(create(Arrays.copyOfRange(inorderArr, i + 1, inorderArr.length), Arrays.copyOfRange(postorderArr, i, postorderArr.length - 1)));
        }
    }
    return node;
}
1
2
3
4
5
int[] inorderArr = {4, 7, 2, 1, 5, 3, 8, 6};
int[] postorderArr = {7, 4, 2, 5, 8, 6, 3, 1};

Node node = create(inorderArr, postorderArr);
System.out.println("node:" + node.getValue());

二叉树的下一个节点

给定一棵二叉树和其中的一个节点，如何找出中序遍历序列的下一个节点？树中的结点除了有两个分别指向左、右子节点的指针，还有一个指向父节点的指针。

思路：
分情况讨论——
（1）给出的节点有右子树，则沿着右子树向下遍历左子节点，最左子节点是下一个节点；

（2）给出的节点没有右子树，如果它是父节点的右子节点，则沿着父节点向上遍历，直到节点是父节点的左子节点，则该节点的父节点是下一个节点；

（3）给出的节点没有右子树，如果它是父节点的左子节点，则父节点是下一个节点。（3）是（2）的特例。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class Node {
    private char value;
    private Node left;
    private Node right;
    private Node parent;

    public Node(char value) {
        this.value = value;
    }

    public char getValue() {
        return this.value;
    }

    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
        left.setParent(this);
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
        right.setParent(this);
    }

    public Node getParent() {
        return parent;
    }

    public void setParent(Node parent) {
        this.parent = parent;
    }
}

public Node inorderNext(Node node) {
    if (node.getRight() != null) {
        node = node.getRight();
        while (node.getLeft() != null) {
            node = node.getLeft();
        }
        return node;
    } else {
        while (node.getParent() != null) {
            if (node.equals(node.getParent().getLeft())) {
                return node.getParent();
            } else {
                node = node.getParent();
            }
        }
        return null;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 初始化二叉树
ArrayList<Node> list = new ArrayList<>(14);
for (int i = 0; i < 14; i++) {
    list.add(new Node((char) ('A' + i)));
}
list.get(0).setLeft(list.get(1));
list.get(0).setRight(list.get(2));
list.get(1).setLeft(list.get(3));
list.get(1).setRight(list.get(4));
list.get(2).setLeft(list.get(5));
list.get(2).setRight(list.get(6));
list.get(3).setRight(list.get(7));
list.get(4).setLeft(list.get(8));
list.get(4).setRight(list.get(9));
list.get(5).setRight(list.get(10));
list.get(6).setLeft(list.get(11));
list.get(6).setRight(list.get(12));
list.get(7).setLeft(list.get(13));

for (Node node : list) {
    System.out.println("node:" + node.getValue() + "; next node:" + ((node = inorderNext(node)) == null ? "null" : node.getValue()));
}

时间复杂度：
空间复杂度：O(1)。

扩展：前序遍历

思路：前序遍历的顺序是节点->左子节点->右子节点。

实现：

1
2
3
4
5
6
7
8
9
public static void preorder(ArrayList<Node> list, Node node) {
    list.add(node);
    if (node.getLeft() != null) {
        preorder(list, node.getLeft());
    }
    if (node.getRight() != null) {
        preorder(list, node.getRight());
    }
}
1
2
3
4
5
ArrayList<Node> preorderList = new ArrayList<>(14);
preorder(preorderList, list.get(0));
for (Node node : preorderList) {
    System.out.println("node:" + node.getValue());
}

扩展：中序遍历

思路：中序遍历的顺序是左子节点->节点->右子节点。

实现：

1
2
3
4
5
6
7
8
9
public static void inorder(ArrayList<Node> list, Node node) {
    if (node.getLeft() != null) {
        inorder(list, node.getLeft());
    }
    list.add(node);
    if (node.getRight() != null) {
        inorder(list, node.getRight());
    }
}
1
2
3
4
5
ArrayList<Node> inorderList = new ArrayList<>(14);
inorder(inorderList, list.get(0));
for (Node node : inorderList) {
    System.out.println("node:" + node.getValue());
}

扩展：后序遍历

思路：后序遍历的顺序是左子节点->右子节点->节点。

实现：

1
2
3
4
5
6
7
8
9
public static void postorder(ArrayList<Node> list, Node node) {
    if (node.getLeft() != null) {
        postorder(list, node.getLeft());
    }
    if (node.getRight() != null) {
        postorder(list, node.getRight());
    }
    list.add(node);
}
1
2
3
4
5
ArrayList<Node> postorderList = new ArrayList<>(14);
postorder(postorderList, list.get(0));
for (Node node : postorderList) {
    System.out.println("node:" + node.getValue());
}

扩展：给定一棵二叉树和其中的一个节点，找出前序遍历序列的下一个节点

思路：
分情况讨论——
（1）给出的节点有左子节点，则下一个节点是该左子节点；
（2）给出的节点没有左子节点，但是有右子节点，则下一个节点是该右子节点；
（3）给出的节点没有子节点，如果它是父节点的右子节点，且有兄弟节点，则下一个节点是兄弟节点；如果它是父节点的右子节点，则沿着父节点向上遍历，直到节点是父节点的左子节点，并且有兄弟节点，则下一个节点是兄弟节点。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public Node preorderNext(Node node) {
    if (node.getLeft() != null) {
        return node.getLeft();
    } else if (node.getRight() != null) {
        return node.getRight();
    } else {
        while (node.getParent() != null) {
            if (node.equals(node.getParent().getLeft()) && node.getParent().getRight() != null) {
                return node.getParent().getRight();
            } else {
                node = node.getParent();
            }
        }
    }
    return null;
}
1
2
3
4
Node node = list.get(0);
while (node != null) {
    System.out.println("node:" + node.getValue() + "; next node:" + ((node = preorderNext(node)) == null ? "null" : node.getValue()));
}

扩展：给定一棵二叉树和其中的一个节点，找出后序遍历序列的下一个节点

思路：
分情况讨论——
（1）给出的节点没有父节点，则下一个节点是 null；
（2）给出的节点有父节点，且是左节点，如果没有兄弟节点，则下一个节点是父节点；否则，找到兄弟节点的最左子节点，如果该节点没有左子节点，但是有右子节点，则继续向下遍历，最后获取的节点就是下一个节点；
（3）给出的节点有父节点，且是右节点，则下一个节点是父节点。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public Node postorderNext(Node node) {
    if (node.getParent() == null) {
        return null;
    } else {
        if (node.equals(node.getParent().getLeft())) {
            if (node.getParent().getRight() == null) {
                return node.getParent();
            } else {
                node = node.getParent().getRight();
                while (node != null) {
                    while (node.getLeft() != null) {
                        node = node.getLeft();
                    }
                    if (node.getRight() == null) {
                        return node;
                    } else {
                        node = node.getRight();
                    }
                }
            }
        } else {
            return node.getParent();
        }
    }
    return null;
}
1
2
3
for (Node node : list) {
    System.out.println("node:" + node.getValue() + "; next node:" + ((node = postorderNext(node)) == null ? "null" : node.getValue()));
}

用两个栈实现队列

用两个栈实现一个队列，分别完成在队列尾部插入节点和在队列头部删除节点的功能。

思路：
队列的特点是先进先出。栈的特点是后进先出，进栈和出栈的顺序相反，如果数据从栈 A 出栈后依次入栈 B，再从栈 B 出栈，则出栈 B 时的顺序和入栈 A 时的顺序是一致的。以此为突破口，即可实现队列。
初始化栈 A、B，栈 A 用于存数据，栈 B 用于取数据。当栈 B 没数据时，会先将栈 A 的数据导入到栈 B，然后再从栈 B 取数据；当栈 B 有数据时，就直接从栈 B 取数据，后续存入栈 A 的数据，等到栈 B 没数据时，在取数据前才从栈 A 导入到栈 B。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Queue<T> {
    private Stack<T> stack1;
    private Stack<T> stack2;

    public Queue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }

    public void push(T t) {
        stack1.push(t);
    }

    public T pop() {
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }

    @Override
    public String toString() {
        return "stack1:" + stack1.toString() + "\nstack2:" + stack2.toString();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Queue<Integer> queue = new Queue<>();
for (int i = 0; i < 20; i++) {
    int random = new Random().nextInt(128);
    if ((random & 4) == 0) {
        try {
            Integer pop = queue.pop();
            System.out.println("pop:" + pop + "\n" + queue.toString());
        } catch (EmptyStackException e) {
            e.printStackTrace();
        }
    } else {
        queue.push(random);
        System.out.println("push:" + random + "\n" + queue.toString());
    }
}

时间复杂度：
空间复杂度：

相关题目：用两个队列实现一个栈

思路：
初始化队列 A、B，两个队列都是用于存/取数据，但是同一时刻，只能有一个队列存数据，另一个队列中的数据为空。当取数据时，将前 n - 1 个数据导入到空队列中，返回倒数第 1 个数据，此时，原来的空队列已经有数据了，以后用于存数据，原来存数据的队列已经被清空了。两个队列交替，总是返回倒数第 1 个数据。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Stack<T> {
    private ArrayDeque<T> queue1;
    private ArrayDeque<T> queue2;
    private ArrayDeque<T> pushQueue;
    private ArrayDeque<T> popQueue;

    public Stack(int capacity) {
        queue1 = new ArrayDeque<>(capacity);
        queue2 = new ArrayDeque<>(capacity);
        pushQueue = queue1;
        popQueue = queue2;
    }

    public void push(T t) {
        pushQueue.addLast(t);
    }

    public T pop() {
        for (int i = 0, size = pushQueue.size(); i < size - 1; i++) {
            popQueue.add(pushQueue.removeFirst());
        }
        if (pushQueue == queue1) {
            pushQueue = queue2;
            popQueue = queue1;
        } else {
            pushQueue = queue1;
            popQueue = queue2;
        }
        return popQueue.removeFirst();
    }

    @Override
    public String toString() {
        return "queue1:" + queue1.toString() + "\nqueue2:" + queue2.toString();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Stack<Integer> stack = new Stack<>(20);
for (int i = 0; i < 20; i++) {
    int random = new Random().nextInt(128);
    if ((random & 6) == 0) {
        try {
            Integer pop = stack.pop();
            System.out.println("pop:" + pop + "\n" + stack.toString());
        } catch (NoSuchElementException e) {
            e.printStackTrace();
        }
    } else {
        stack.push(random);
        System.out.println("push:" + random + "\n" + stack.toString());
    }
}

斐波那契数列

求斐波那契数列的第 n 项。

思路：
递归由于多次重复计算，所以效率低。可以使用循环，由下向上计算。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int fibonacci(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        int preTwo = 0;
        int preOne = 1;
        int value = 0;
        for (int i = 2; i <= n; i++) {
            value = preTwo + preOne;
            preTwo = preOne;
            preOne = value;
        }
        return value;
    }
}
1
2
3
for (int n = 0; n < 10; n++) {
    System.out.println("fibonacci[" + n + "]:" + fibonacci(n));
}

时间复杂度：O(n)。
空间复杂度：O(1)。

题目二：青蛙跳台阶问题

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

思路：
把 n 级台阶时的跳法看成 n 的函数，计为 f(n)，当 n > 2 时，如果第一次跳 1 级，则跳法数目等于剩余 n - 1 级台阶的跳法数目，即 f(n - 1)；如果第一次跳 2 级，则跳法数目等于剩余 n - 2 级台阶的跳法数目，即 f(n - 2)；因为第一次只能跳 1 级或 2 级，所以 f(n) = f(n - 1) + f(n - 2)，就是上面的斐波那契数列了。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int jump(int n) {
    if (n == 1) {
        return 1;
    } else if (n == 2) {
        return 2;
    } else {
        int preTwo = 1;
        int preOne = 2;
        int value = 0;
        for (int i = 3; i <= n; i++) {
            value = preTwo + preOne;
            preTwo = preOne;
            preOne = value;
        }
        return value;
    }
}
1
2
3
for (int n = 1; n < 10; n++) {
    System.out.println("jump[" + n + "]:" + jump(n));
}

本题扩展：青蛙跳 n 级台阶时，一次最多可以跳 n 级

在青蛙跳台阶的问题中，如果把条件改成：一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶……它也可以跳上 n 级，此时该青蛙跳上一个 n 级的台阶总共有多少种跳法？我们用数学归纳法可以证明 f(n) = 2^(n - 1)。

思路：
因为 f(n) = 2^(n - 1)，所以 f(n - 1) = 2[1] = 2^(n - 1) * 2^(-1)，也就是说 f(n) 是 f(n - 1) 的 2 倍。

实现：

1
2
3
4
5
6
7
8
9
10
11
public static int jump(int n) {
    if (n == 1) {
        return 1;
    } else {
        int value = 1;
        for (int i = 1; i < n; i++) {
            value *= 2;
        }
        return value;
    }
}
1
2
3
for (int n = 1; n < 10; n++) {
    System.out.println("jump[" + n + "]:" + jump(n));
}

相关题目：用 2 x 1 的小矩形横着或者竖着去覆盖 2 x n 的大矩形

我们可以用 2 x 1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2 x 1 的小矩形无重叠地覆盖一个 2 x n 的大矩形，总共有多少种方法？

思路：
当小矩形竖着放时，剩余面积是 2 x (n - 1)；当小矩形横着放时，小矩形下方也是惟一确定可以放一个小矩形，剩余面积是 2 x （n - 2）；所以 f(n) = f(n - 1) + f(n - 2)。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int jump(int n) {
    if (n == 1) {
        return 1;
    } else if (n == 2) {
        return 2;
    } else {
        int preTwo = 1;
        int preOne = 2;
        int value = 0;
        for (int i = 3; i <= n; i++) {
            value = preTwo + preOne;
            preTwo = preOne;
            preOne = value;
        }
        return value;
    }
}
1
2
3
for (int n = 1; n < 10; n++) {
    System.out.println("jump[" + n + "]:" + jump(n));
}

  1. (n - 1) - 1 ↩︎

《剑指 Offer》算法题（10/68）
https://weichao.io/db7d7a2f7b38/
作者
魏超
发布于
2020年3月16日
更新于
2022年12月4日
许可协议